Rumus-rumus dalam berbagai hitungan matematika seperti rumus keliling lingkaran, luas lingkaran dan persamaan garis lurus memang banyak digunakan dalam kehidupan sehari-hari. Selain rumus di atas, rumus volume tabung juga memberikan manfaat bagi kehidupan masyarakat. Untuk memahami volume tabung, anda bisa menggunakan berbagai benda yang ada disekitar anda seperti misalnya gelas yang panjang dan berbentuk silinder. Selain itu anda juga dapat menggunakan drum, toples, kaleng susu, gas elpiji dan lain sebagainya.
Ada banyak sekali benda-benda yang berbentuk tabung yang dapat anda temukan. Dengan menggunakan barang-barang tersebut, terutama gelas, toples dan kaleng susu dapat mempermudah anda dalam mengetahui volume tabung. Cara mudahnya adalah anda tinggal mengisi gelas tersebut dengan air, lalu mengukur volume air dalam gelas dengan wadah yang sudah memiliki ukuran seperti gelas ukur dan lain sebagainya. Namun sebelumnya anda harus mengenal tabung terlebih dahulu agar lebih mudah dalam mempelajarinya.
Definisi Tabung atau Silinder
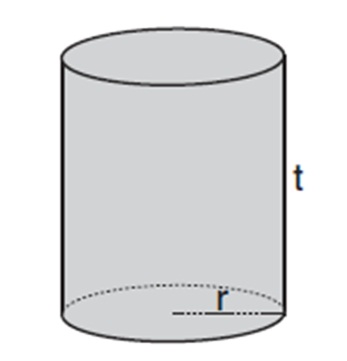
Tabung atau silinder adalah bangun ruang 3 dimensi, tidak seperti lingkaran yang merupakan bangun 2 dimensi. Tabung memiliki permukaan yang berbentuk lingkaran, yaitu di bagian atas dan juga di bagian bawah, dan kedua lingkaran tersebut saling terhubung dengan sebuah sisi tegak melengkung atau selimut yang berbentuk persegi panjang yang akan menutupi bagian tegak tabung tersebut. Akan lebih mudah mengerjakan rumus volume tabung apabila anda mengenal bagian-bagian tabung dengan baik. Oleh sebab itu anda harus mengenal tabung, mulai dari unsur dan sifat dari tabung.
- Unsur-unsur tabung
- Memiliki 3 sisi, bagian atas, bawah dan sisi lengkung.
- Memiliki 2 rusuk, yaitu rusuk bagian atas dan bawah.
- Tidak memiliki sudut.
- Sifat-sifat tabung
- Sisi atas dan bawah berupa lingkaran dengan jari-jari yang sama panjang.
- Tinggi tabung merupakan jarak antara titik pusat lingkaran sisi atas dengan titik pusat lingkaran sisi bawah.
- Tabung memiliki 9 pola jaring-jaring.
- Panjang selimut tabung adalah keliling dari sisi atas atau sisi bawah tabung, yaitu 2πr.
Rumus Volume Tabung dan Kegunaannya
Banyak yang mengatakan bahwa menghafal rumus volume tabung tidak memiliki manfaat karena tidak akan digunakan dalam kehidupan sehari-hari. Sebenarnya penggunaan rumus-rumus matematika tersebut tergantung dari pekerjaan yang anda lakukan. Apabila anda bekerja dalam bidang konstruksi bangunan atau arsitek, tentu anda membutuhkan kemampuan matematika yang baik agar dapat membangun rumah dengan baik. Jika anda bekerja di sebuah pabrik minuman, anda pun nantinya akan menggunakan rumus matematika terutama untuk mengetahui berapa banyak soda yang harus dimasukkan ke dalam kaleng berbentuk silinder dengan tinggi dan diameter tertentu agar kaleng tersebut penuh terisi dengan soda.
Karena itulah apabila ada orang yang mengatakan rumus matematika tidak berguna, sebenarnya hal tersebut tergantung dari persepsi masing-masing orang. Baru akan terasa apakah pelajaran yang selama ini anda pelajari di bangku sekolah akan bermanfaat di kehidupan sehari-hari atau tidak adalah ketika anda sudah lulus kuliah dan masuk ke dalam dunia kerja. Lalu seperti bagaimana caranya mencari volume sebuah tabung? Caranya sangatlah mudah, anda tinggal memasukkan data-data yang anda temukan ke dalam rumus, Volume = π x r2 x tinggi. Misalnya saja sebuah tabung memiliki jari-jari alas sebesar 5 cm dan tingginya 10 cm. Untuk mencari volumenya anda tinggal memasukkan r dan tinggi tabung tersebut ke dalam rumus yang ada. Volume = 3,14 x 52cmx10 cm, didapatkan volume tabung tersebut sebesar 785 cm3.